线性表 | DS
定义和基本操作
线性表
具有相同数据类型的 $n$ 个数据元素的有限序列($n \geq 0$)。
空表:表长 $n$ 为 0
线性表的逻辑特性
⚠表中元素的个数有限。
⚠表中元素具有逻辑上的顺序性,表中元素有其先后顺序。
表中元素都是数据元素,每个元素都是单个元素。
表头元素唯一,表尾元素唯一。
表头无前驱,表尾无后继。
除表头表尾,每个元素有且仅有一个直接前驱和一个直接后继。
⚠表中元素的数据类型都相同(意味着每个元素占有相同大小的存储空间)。
线性表的基本操作
初始化、求表长、判空、插入、删除、按值查找、按位查找、打印、销毁。
存储结构
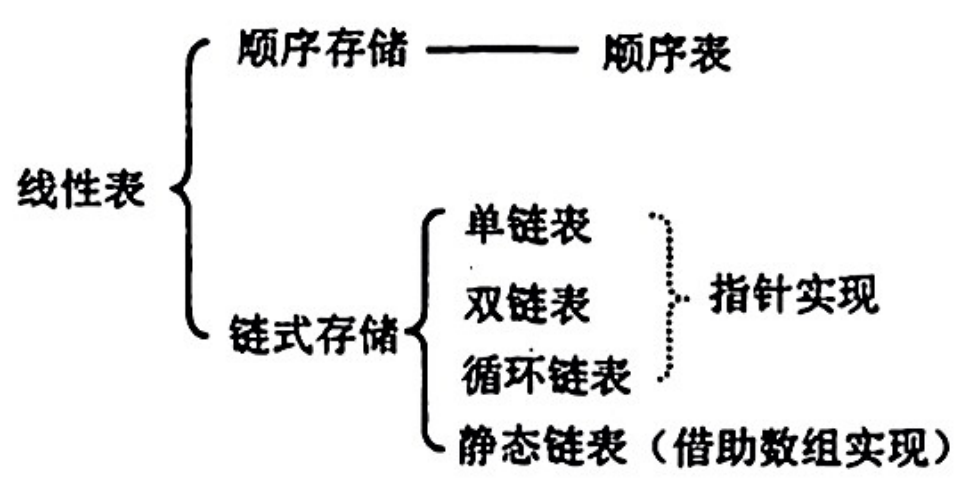
顺序表示
顺序表
线性表的顺序存储又称顺序表。
顺序表的特点
表中元素的逻辑顺序与其物理顺序相同;
每个数据元素的存储位置都和线性表的起始位置相差一个和该数据元素的位序成正比的常数;
通过首地址和元素序号可在时间 O(1) 内找到指定的元素,即可随机存取。
通常用高级程序设计语言中的数组来描述线性表的顺序存储结构。
线性表中元素的位序从 1 开始,数组中元素下标从 0 开始。
存储空间连续,分配只能预先进行;
存储密度高,每个结点只存储数据元素。
顺序表的优点
- 可随机访问;
- 存储密度高。
顺序表的缺点
- 元素的插入和删除需要移动大量的元素;
- 顺序存储分配需要一段连续的存储空间,不够灵活,还可能造成存储空间的浪费。
链式表示
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。因此为了表示每个数据元素与其直接后继之间的逻辑关系,除了存储其本身的信息之外,还需(至少)存储一个指示其直接后继的信息(即直接后继的存储位置)。
单链表
单链表/线性链表
结点:数据元素的存储映像,包括存储数据元素信息的数据域和存储直接后继位置的指针域。
$n$ 个结点链结成一个链表,即为线性表的链式存储结构。由于此链表中的每个结点只包含一个指针域,故称线性链表或单链表。
单链表的特点
- 非随机存取;
- 元素离散地分布在存储空间;
- 存储空间利用率稍低。
“第一个” 结点
开始结点:存储有第一个数据元素的结点。
头结点:数据域可以不存储信息,也可存储一些描述链表属性的信息;指针域存储指向开始结点的指针。
第一个结点:头结点/开始结点。
头指针:指向第一个结点,通常用作链表的标识。
头结点的引入,方便了运算的实现:
- 对第一个元素的操作和对其他位置上元素的操作一致,无需特殊处理,算法统一;
- 空表和非空表的处理也得到统一(无论链表是否为空,其头指针都是指向头结点的非空指针)。
⚠注意:表长不计头结点。
单链表的插入与删除
单链表结点只有一个指向其后继的指针,使得单链表只能从前往后依次的单向遍历。单链表通用的插入和删除操作都需要找到相应的前驱结点,只能从头开始遍历,访问前驱的时间复杂度为 O(n),因此插入和删除操作的时间复杂度也都为 O(n)。
在拥有待删除结点的指针以及其后继结点存在的情况下,可根据其后继结点删除该结点,这种删除操作的时间复杂度为 O(1)。
只是头插的话,时间复杂度是 O(1)。
🌱与顺序表插入与删除的对比
在顺序表中进行插入、删除操作时,平均移动表中一半的元素,时间复杂度为 O(n),当数据元素的信息量较大且表较长时,这一点是不应忽视的;在链表中进行插入和删除操作时,虽然时间复杂度也是 O(n),但操作主要是比较操作,从这个角度考虑显然后者优于前者。
双链表
双链表可以很方便地找到其前驱结点,因此插入删除的时间复杂度仅为 O(1)(单链表插入删除操作时间复杂度为 O(n) 时是因为花了 O(n) 去找前驱结点了)。
插入结点的语句顺序注意下,不要着急把 p->next 改了。
循环链表
循环单链表
正因循环单链表是一个 “环”,所以在任何位置上的插入和删除操作都是等价的,无须判断是否是表尾。
有时不设头指针而仅设尾指针,这样尾插也和头插一样只需要 O(1) 的时间复杂度。但删除尾结点依然麻烦,因为还是需要遍历找到尾结点的前驱结点。
所以对于经常删除尾结点的线性表,直接排除(循环)单链表和不带尾结点指针的非循环双链表。
循环单链表和单链表所占内存空间相同。
判空:头结点的 next 指针是否等于头指针。
循环双链表
判空:头结点的 prior 和 next 指针是否都等于头指针。
静态链表
使用数组来描述线性表的链式存储结构。
结点也有数据域 data 和指针域 next,这里的指针是结点的相对地址(数组下标),又称游标。
实质是一维结构体数组。
显然,和顺序表一样,静态链表也要预先分配一块连续的内存空间。
顺序表 vs 链表
两种存储结构各有长短,选择哪一种由实际问题的主要因素决定(重点论)。
通常较稳定的线性表选择顺序存储,而频繁进行插入和删除操作的线性表(即动态性较强)宜选择链式存储。
刷题
顺序表可以利用一维数组表示,因此顺序表与一维数组在逻辑结构上是相同的❌
一维数组中的元素可以不连续存放;
一维数组只是一种存储结构,不对应任何逻辑结构,栈、队列和树等逻辑结构也可利用一维数组表示,而顺序表是线性表的顺序存储,是一种数据结构。
链式存储设计时,各个不同结点的存储空间可以不连续,但结点内的存储单元地址必须连续。
若用单链表来表示队列,则应该选用带尾指针的循环链表。
队列需要在表头删除元素,表尾插入元素,采用带尾指针的循环链表较为方便,插入和删除的时间复杂度都为 O(1)。
涉及删除操作的线性表链式存储结构的选取,基本上就是看能不能直接找到要删除结点的前驱结点。
头结点是开始结点的前驱结点。
