树 | DS
树
基本概念
树的定义
树是 $n$($n \ge 0$)个结点的有限集。当 $n=0$ 时,称为空树。
任意非空树由唯一根结点与若干棵互不相交的子树组成(每一棵子树又是一棵树,递归定义)。
树作为一种逻辑结构,同时也是一种分层结构。
树的特点
根结点无前驱,其他所有结点有且只有一个前驱。
树中所有结点可以有零个或多个后继。
基本术语
空树、结点的度(结点的孩子个数)、树的度(树中结点的最大度数)、叶子/终端结点(度为 0)、分支/非终端结点(度大于 0)、内部结点、孩子、双亲、兄弟、堂兄弟(双亲在同一层)、祖先、子孙、层次(根结点为第 1 层)、树的高度/深度(树中结点的最大层数)、结点深度(自顶向下逐层累加)、结点高度(自底向上逐层累加)、有序树(树中结点的各子树左右有序,不能互换)、无序树、路径(结点序列)、路径长度(路径上所经过的边的个数)、丰满树/理想平衡树(除最底层外其他层都是满的)、森林(若干棵互不相交的树的集合)。
⚠分支有向(从双亲指向孩子),路径只能自顶向下,故同一双亲的两个孩子之间不存在路径。
“路径长度”
- 结点的路径长度:根到该结点经过的边数。
- 树的路径长度:所有结点的路径长度之和。
- 结点的带权路径长度:该结点路径长度与其权值的乘积。
- 树的带权路径长度 WPL:所有叶结点的带权路径之和。
树的性质
总结点数 $n$ = 总分支数 + 1 = 所有结点的度之和 + 1
$n = n_0+n_1+n_2+n_3+…+n_m = 1+n_1+2n_2+3n_3+…+mn_m$
$n_0=1+n_2+2n_3+…+(m-1)n_m$
度为 $m$ 的树中第 $i$ 层上至多有 $m^{i-1}$ 个结点。
高度为 $h$ 的 $m$ 叉树至多有 $(m^h-1)/(m-1)$ 个结点。
具有 $n$ 个结点的 $m$ 叉树的最小高度为 $\lceil \log_m(n(m-1)+1) \rceil$。
度为 $m$、具有 $n$ 个结点的树的最大高度为 $n-m+1$。
高度为 $h$、度为 $m$ 的树至少有 $h+m-1$ 个结点。
存储结构
双亲表示法(顺序)
最简单直观。
利用了每个结点(根结点除外)双亲唯一的性质,可以很快得到每个结点的双亲结点,但求结点的孩子时需要遍历整个结构。
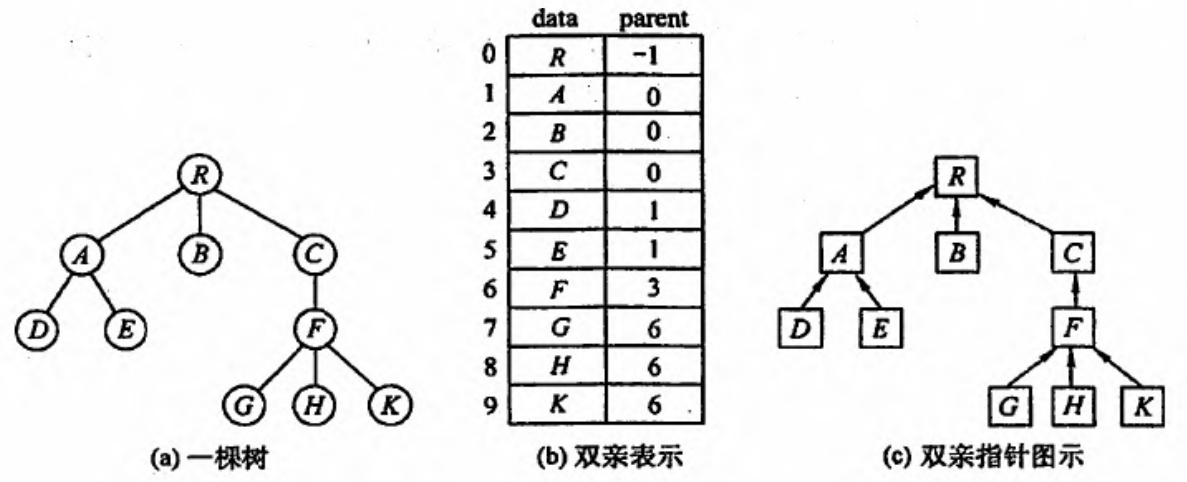
⚠注意区别树的顺序存储结构与二叉树的顺序存储结构。
在树的顺序存储结构中,数组下标代表结点编号,下标中所存内容指示结点之间的关系;而在二叉树的顺序存储结构中,数组下标既代表了结点的编号,又指示了二叉树中各结点之间的关系。
二叉树属于树,因此二叉树也可用树的存储结构来存储,但树却不能用二叉树的存储结构来存储。
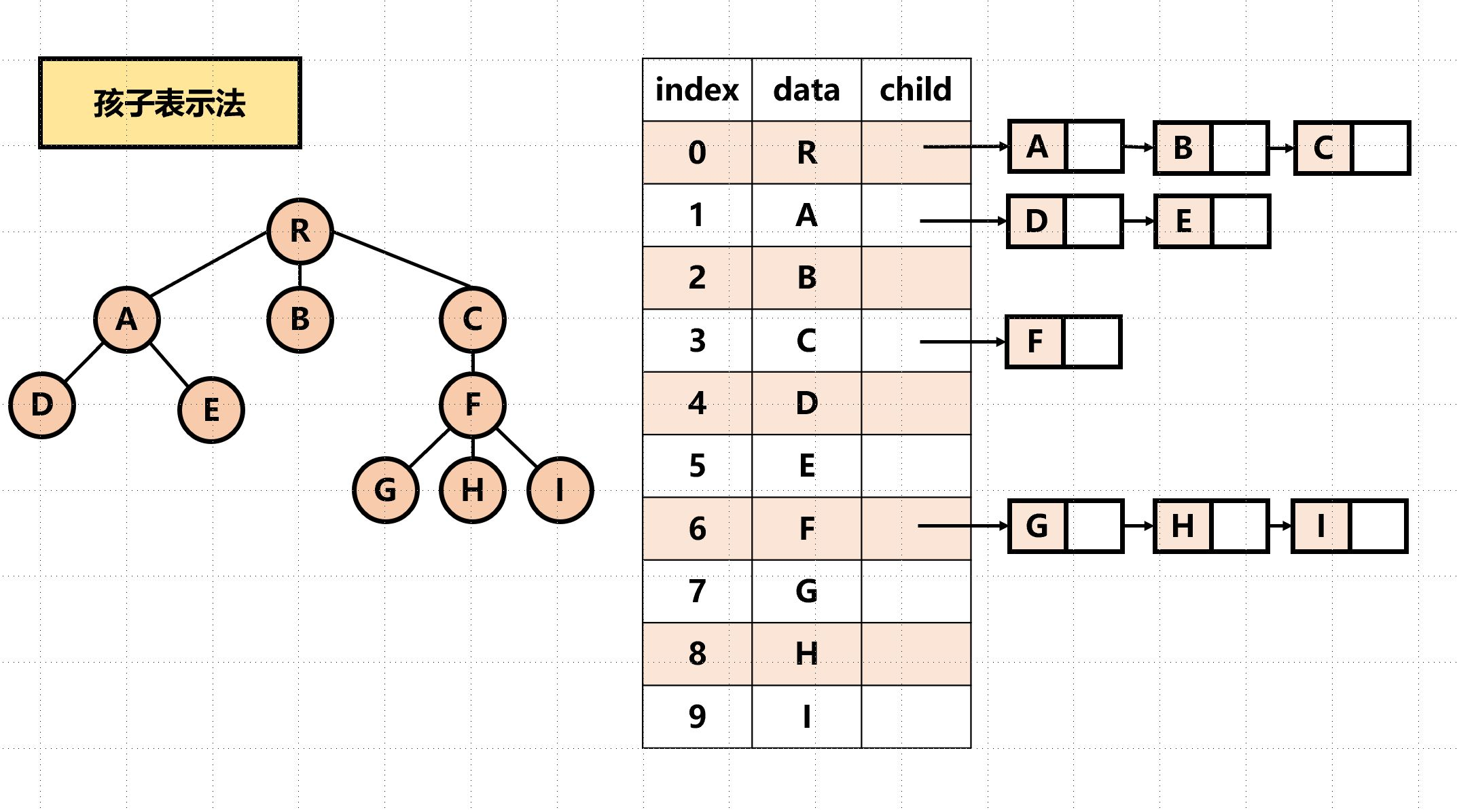
孩子表示法(顺序 + 链式)
实质是图的邻接表存储结构。
找孩子简单;找双亲麻烦,需要遍历 $n$ 个结点中孩子链表指针域所指向的 $n$ 个孩子链表。
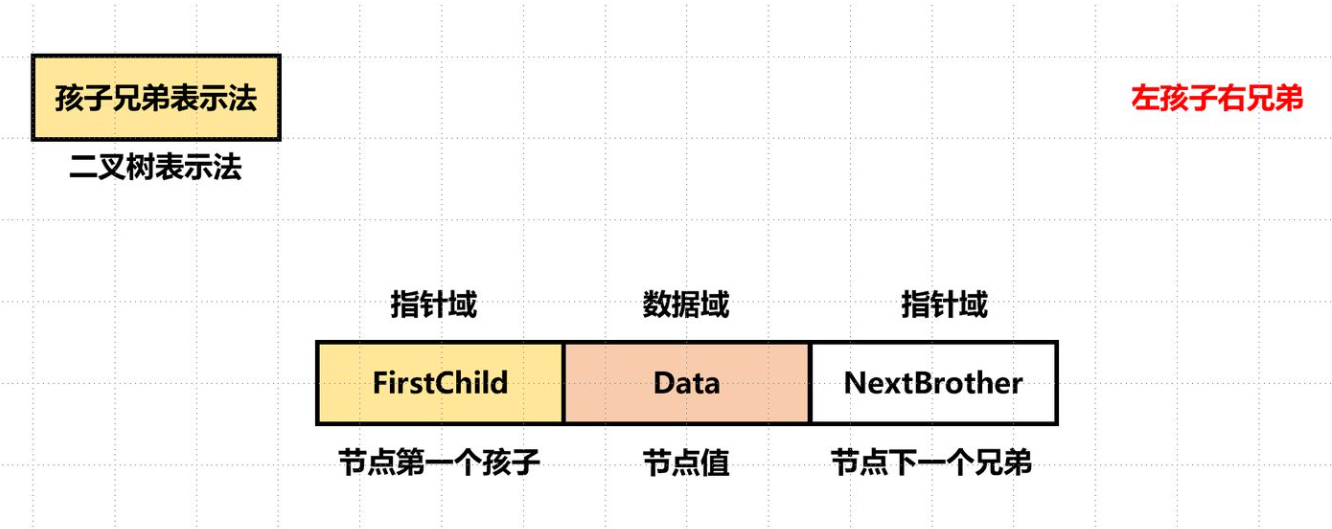
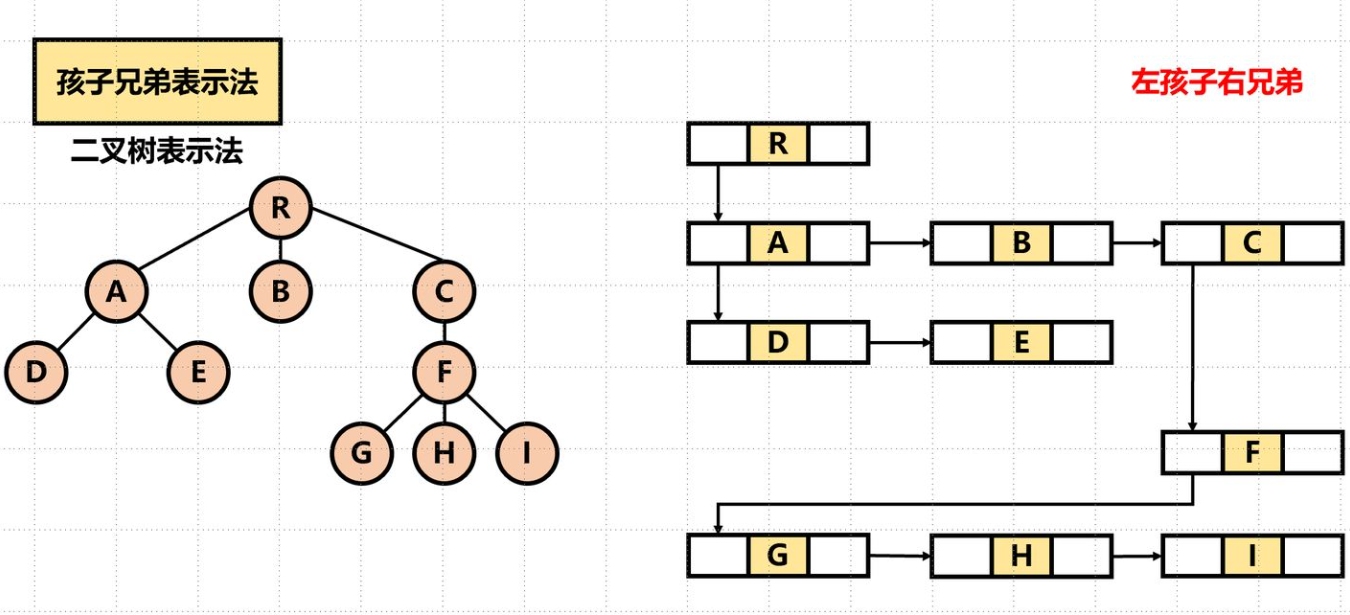
孩子兄弟表示法/二叉树表示法
每个结点包括三部分内容:结点值、指向结点第一个孩子结点的指针、指向结点下一个兄弟结点的指针(沿此域可以找到结点的所有兄弟结点)。
可以方便地实现树转换为二叉树的操作、易于查找孩子等。
找双亲也还是麻烦(除非再加个 parent 指针)。
二叉树
基本概念
二叉树的定义
对树的限制:每个结点最多两棵子树,并且二叉树的子树有左右之分,其次序不能任意颠倒。
二叉树的基本形态(5 种)
空二叉树、只有根结点、只有左子树、只有右子树、左右子树都有。
二叉树 vs 度为 2 的有序树
1)二叉树是度最多为 2,可为空;度为 2 的有序树至少有 3 个结点。
2)二叉树的结点次序不是相对于另一结点而言,而是确定的;有序树的结点次序是相对于另一结点而言的,如果有序树中的子树只有一个孩子,那这个孩子结点就无须区分其左右次序。
特殊的二叉树
1)满二叉树:高度为 $h$,且含有 $2^h-1$ 个结点的二叉树。
2)完全二叉树:对应相同高度的满二叉树缺失最下层最右边的一些连续叶结点。
3)二叉排序树:左子树所有结点的关键字均小于根结点的关键字;右子树所有结点的关键字均大于根结点的关键字;左右子树又各是一棵二叉排序树。
4)平衡二叉树:任意一个结点的左右子树深度之差不超过 1。
5)正则二叉树:树中每个分支节点都有 2 个孩子,即树中只有度为 0 或 2 的结点。可推广至正则 $k$ 叉树。
主要特性
二叉树性质
$n = n_0+n_1+n_2 = 1+n_1+2n_2$
$n_0=1+n_2$
$n_0$ 和 $n_2$ 奇偶性相反,$n_0+n_2$ 必为奇数。
第 $i$ 层最多 $2^{i-1}$ 个结点($i≥1$)。
高度/深度为 $k$ 的二叉树最多有 $2^{k}-1$ 个结点($k≥1$)。
含有 $n$ 个结点的二叉链表中含有 $2n-(n-1) = n+1$ 个空链域。
完全二叉树特点
对于有 $n$ 个结点的完全二叉树,$i$ 为某结点 $a$ 的编号(从上到下、从左到右依次编号 $1,2,…,n$):
若 $i≠1$,则 $a$ 双亲结点编号 $\lfloor i / 2\rfloor$;
若 $2i≤n$,则 $a$ 左孩子标号为 $2i$;
若 $2i+1≤n$,则 $a$ 右孩子标号为 $2i+1$。
若 $i ≤ \lfloor n / 2\rfloor$,则结点 $i$ 为分支结点,否则为叶结点。
二叉树 $n_0+n_2$ 必为奇数。对于完全二叉树,$n_1$ 只能为 0 或 1。若 $n$ 为奇数,则完全二叉树的每个分支结点都有左孩子右孩子;若 $n$ 为偶数,则编号最大的分支结点(编号为 $n/2$)只有左孩子,其余分支结点都有左孩子右孩子。
具有 $n$ ($n≥1$) 个结点的完全二叉树的高度/深度为 $\left\lceil\log _2(n+1)\right\rceil$ 或 $\left\lfloor\log _2 n\right\rfloor+1$。
结点 $i$ 所在层次(深度)为 $\left\lceil\log _2(i+1)\right\rceil$ 或 $\left\lfloor\log _2 i\right\rfloor+1$。
叶结点只可能在层次最大的两层出现。对于最大层次中的叶结点,都依次排列在该层最左边的位置上。
若有度为 1 的结点,则只可能有一个,且该结点只有左孩子。
若某结点为叶结点或只有左孩子,则编号大于该结点的结点均为叶结点。
存储结构
顺序存储结构
用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即完全二叉树上编号为 $i$ 的结点元素存储在一维数组下标为 $i-1$ 的分量中。
为了利用完全二叉树特点 1,可从数组下标 1 开始存储树中的结点,保证数组下标和结点编号一致。
对于一般的二叉树,为了让数组下标能反映二叉树结点之间的逻辑关系,只能添加一些并不存在的空结点,让其每个结点与完全二叉树上的结点相对照,再存储到一维数组的相应分量中。
考虑到空间利用率,顺序存储结构比较适合完全二叉树和满二叉树。
链式存储结构
二叉链表,结点至少三个域:数据域、左指针域、右指针域。
在含有 $n$ 个结点的二叉链表中,含有 $n+1$ 个空链域
在实际应用中,还可以增加某些指针域,如增加指向父结点的指针后,变成三叉链表的存储结构。
遍历
二叉树的遍历是指按某条搜索路径访问树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。
按照先遍历左子树后右子树的原则,常见的遍历次序有先序 NLR、中序 LNR 和后序 LRN 三种。
其中 “序” 指的是根结点何时被访问,N、L、R 分别指根结点 Node、左子树 Left subtree、右子树 Right subtree。
深度优先遍历
先序遍历
第一个结点:根结点。
最后一个结点:最右叶结点。
规律:祖先先访问(直系),同辈则最左。
中序遍历
第一个结点:最左。
最后一个结点:最右。
遍历规律:左方先访问。
后序遍历
第一个结点:最左叶结点。
最后一个结点:根结点。
遍历规律:子孙先访问(直系),同辈则最左。
其他特点:
三种遍历的统一规律:① 左子树 → 右子树;② 所有叶结点顺序相同。
先序/后序/层次 + 中序,可唯一确定一棵二叉树。
三种遍历的递归算法的递归过程都是一致的:

使用后序非递归遍历算法可以得到祖先到子孙的路径
在后序非递归遍历算法中,访问一个结点 p 时,栈中结点恰好是结点 p 的所有祖先,从栈底到栈顶结点再加上结点 p,刚好构成从根节点到结点 p 的一条路径。
在很多算法设计中都可以利用这一思路来求解,如求两个结点的最近公共祖先等。
以先序序列为入栈次序,中序序列为相应的出栈次序(随时可出)
给定 $n$ 个结点的先序序列,可以构成 $h(n)=\frac{C^n_{2n}}{n+1}$ 种不同的二叉树。
层次遍历/广度优先遍历
需借助一个队列。
由遍历序列构造二叉树
由先/后序序列和中序序列构造一棵二叉树
观察法:在中序划根,得到当前根的左右子树,边划边结合先序。
知先序,找不可能的中序
除了前面说的观察法,还根据先序序列和中序序列的关系:以先序序列为入栈次序,中序序列为出栈次序(随时可出)。
知先后
可推祖先和子孙关系:先序 X……Y,后序 Y……X,则 X 是 Y 祖先(X、Y 可以是一坨结点)。
先后序列完全相反 $\rightarrow$ 二叉树高度等于结点数。
先序 NLR 与后序 LRN 相反:L 或 R 为空,每层只有一个结点(即该二叉树高度等于其结点数/只有一个叶结点)。
先序 NLR 与后序 LRN 相同:L、R 都空(即只有根结点)。
先序 NLR 与中序 LNR 相同:所有非叶结点没有左子树。
前提是非空二叉树。
线索二叉树
规定:若无左子树,就令
lchild指向其前驱结点;若无右子树,就令rchild指向其后继结点。每个结点还需增加两个标志域标识指针域是指向孩子还是线索。引入目的
加快查找结点前驱和后继的速度(前驱后继源自深度优先遍历)。
实现基础
在含 $n$ 个结点的二叉树中,有 $n+1$ 个空指针,利用这些空链域来存放指向其前驱或后继的指针,这样就能像遍历单链表那样方便地遍历二叉树。
原 $n+1$ 个空链域全部成为了线索,但线索仍可能是空链域。
二叉树线索化后仍不能解决:先序求前驱、后序求后继
中序前驱:左线索/左子树最右结点。
中序后继:右线索/右子树最左结点。
先序前驱:为其双亲(自己为双亲的左孩子或自己为双亲的右孩子但无左兄弟时)或是左兄弟树最右叶结点(自己为双亲的右孩子且有左兄弟时)。都需要找到双亲,要是自己有左孩子(即无左线索),就无法找到。
先序后继:左孩子/右孩子/右线索。
后序前驱:右孩子/左孩子/左线索。
后序后继:(除了根结点后继为空的情况)为其双亲(自己为双亲的右孩子或自己为双亲的左孩子但无右兄弟时)或是右兄弟树最左叶结点(自己为双亲的左孩子且有右兄弟时)。都需要找到双亲,要是自己有右孩子(即无右线索),就无法找到。
可见先序求前驱、后序求后继都需要找到双亲结点。可采用三叉链表解决,即每个结点内增加一个指向双亲结点的指针,或借助栈的支持。
后序线索二叉树的遍历仍需要采用三叉链表或栈的支持,因为某结点要是有右孩子(即无右线索)是无法直接找到后序的后继结点的。
中序线索二叉树的构造
线索化的实质是深度优先遍历一次二叉树。
中序线索二叉树的遍历
可以拆分成两个算法:
1)找到中序序列中的第一个结点(最左结点)。
2)找到某结点在中序序列下的后继(右线索/右子树最左结点)。
带头结点的中序线索二叉树
头结点
lchild指向二叉树根结点,rchild指向中序遍历时访问的最后一个结点,同时令中序序列第一个结点的lchild和最后一个结点的rchild均指向头结点。这好比为二叉树建立了一个双向循环线索链表,方便从前往后或从后往前对线索二叉树进行遍历。
树、森林
转换
从物理结构上看,树的孩子兄弟表示法与二叉树的二叉链表表示法是相同的,因此可以用同一存储结构的不同解释将一棵树转换为二叉树。
树 → 二叉树
兄弟结点之间连线、每个结点只保留它与第一个孩子的连线、以树根为轴顺时针旋转 45°。
根结点右子树必为空。
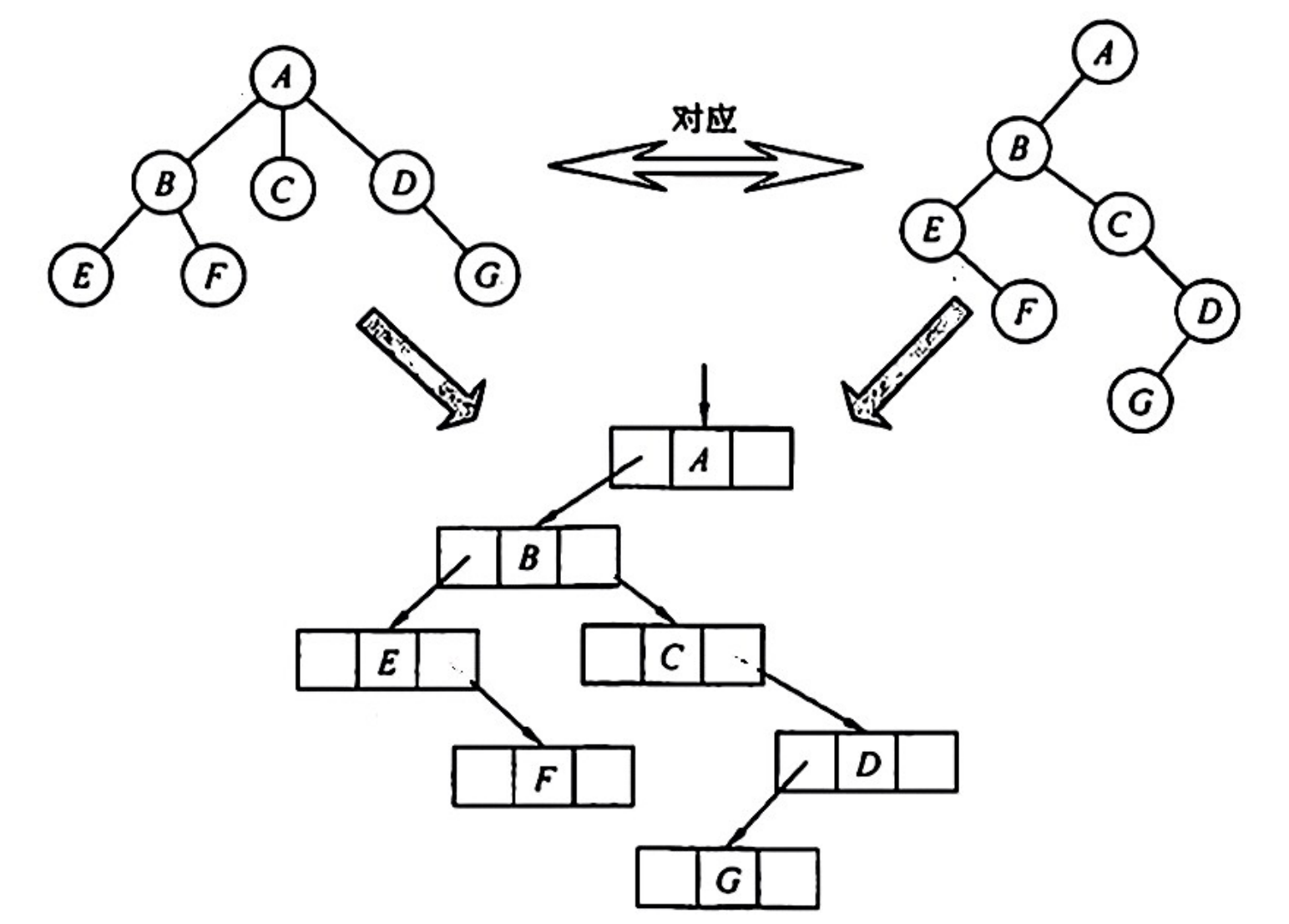
二叉树 → 树
调整水平,连层间,去层内。
森林 → 二叉树
每棵树先转成二叉树,最后每棵二叉树的根结点从左往右依次连接(每棵树的根视为兄弟关系)。
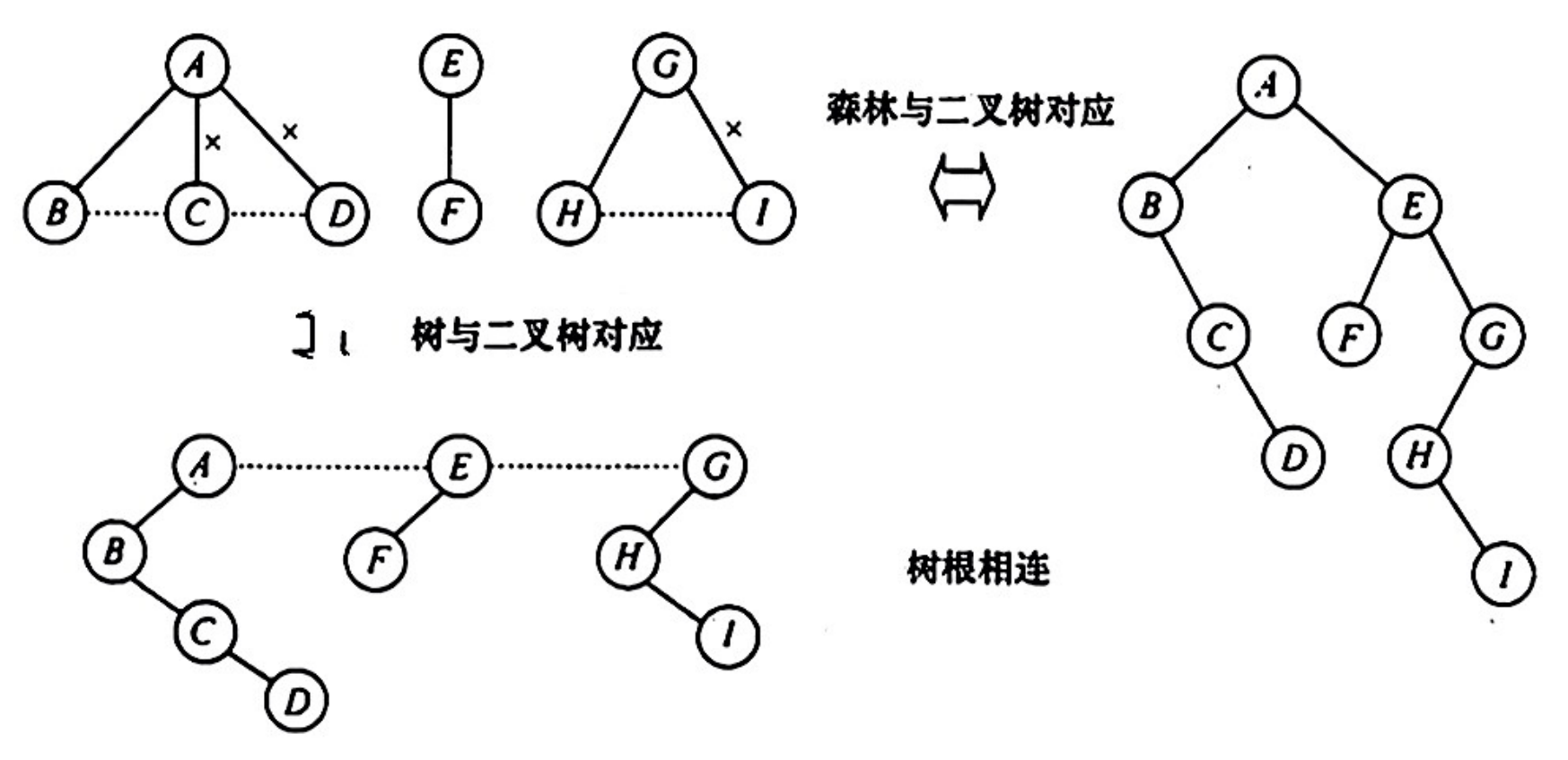
二叉树 → 森林
根的右链依次断开,拆成若干没有右子树的二叉树,然后再将这些二叉树转成树。
👉二叉树转换为树或森林是唯一的。
遍历
树的遍历
先根遍历:先根后子树。其遍历序列与对应二叉树的先序序列相同。
后根遍历:先子树后根。其遍历序列与对应二叉树的中序序列相同。
层序遍历:从上往下逐层访问。
森林的遍历
先序遍历:从左往右依次先根遍历每棵树。其遍历序列与对应二叉树的先序序列相同。
中序遍历/后序遍历:从左往右依次后根遍历每棵树。其遍历序列与对应二叉树的中序序列相同。
称中序遍历是相对于其对应二叉树而言,称后序是因为根是最后访问的。
应用
哈夫曼树
权
在许多应用中,树中结点常常被赋予一个表示某种意义的数值,称为该结点的权。
结点的带权路径长度
从树的根到任意结点的路径长度(经过的边数)与该结点上权值的乘积。
树的带权路径长度 WPL
树中所有叶结点的带权路径长度之和(也等于其所有分支结点的权值之和)。
哈夫曼树/最优 k 叉树
在含有 $n$ 个带权叶结点的 $k$ 叉树中,带权路径最小的 $k$ 叉树。
考题一般默认哈夫曼树是二叉树。
哈夫曼树的构造
1)找权值最小的 $k$ 个根作为子树构成一棵新的 $k$ 叉树,该 $k$ 叉树根结点的权值为其子树根结点权值之和。
2)重复第一步,直到只剩下一棵 $k$ 叉树。
当初始叶结点个数 $n_0$ 满足 $u = (n_0 - 1) \% (k - 1) = 0$ 时才可构造出 $k$ 叉哈夫曼树。当不满足时,需补上 $k-1-u$ 个权值为 $0$ 的虚叶结点。
每构造一个度为 $k$ 的结点,就会少 $k - 1$ 坨结点,直到最后剩下 1 大坨结点。
显然,哈夫曼二叉树不需要补虚叶结点。
哈夫曼 $k$ 叉树的特点
1)树的带权路径长度最短(即 WPL 最小)。
2)孩子结点权值之和等于父结点权值。
3)所有初始结点最终都成为叶结点,且权值越大的结点离根结点越近。
4)哈夫曼树任一分支结点的权值一定不小于下一层任一结点的权值。
5)其结点的度只有 $0$ 与 $k$ 两种 → 正则/严格 $k$ 叉树,$n_0 = 1+(k-1)n_k$。
6)构造过程中共新建了 $(n_0-1)/(k-1)$ 个结点(即 $n_k$)。
7)对应一组权值构造出来的哈夫曼树一般不是唯一的:左右孩子结点的顺序是任意的。此外,如有若干权值相同的结点,则构造出的哈夫曼树更可能不同。但 WPL 必然相同且是最优的。
哈夫曼编码
特点:
1)可变长度:允许对不同字符用不等长的二进制位表示。
2)数据压缩:可变长度编码对频率高的字符赋以短编码,而对频率较低的字符赋以较长一些的编码,从而可以使字符的平均编码长度减短,起到压缩数据的效果。
3)前缀编码:没有一个编码是另一个编码的前缀。
由哈夫曼二叉树构造哈夫曼二进制编码的示例:
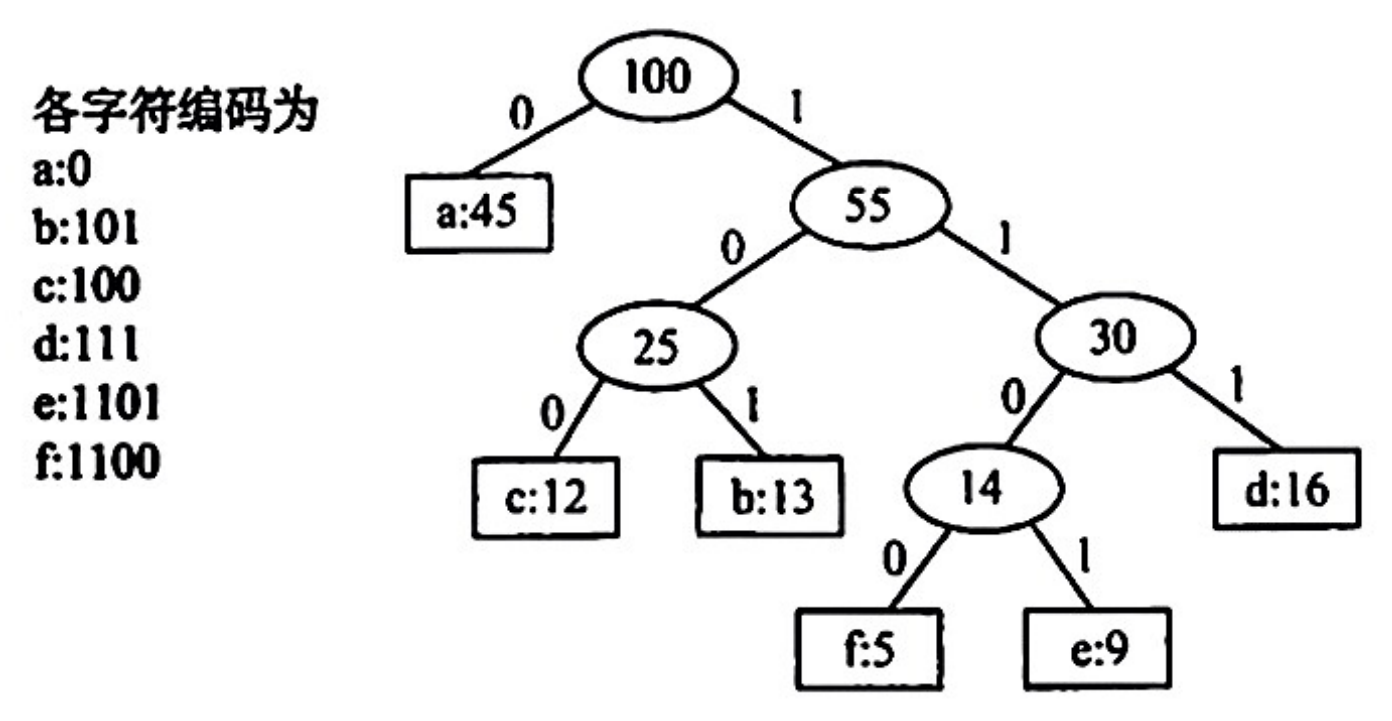
将每个字符当作一个独立的结点,其权值为它出现的频率或次数,构造出对应的哈夫曼树。显然所有字符结点都出现在叶结点中。可将字符的编码解释为从根至该字符路径上边标记的序列,其中边标记为 0 表示 ”转向左孩子“,边标记为 1 表示 ”转向右孩子“(左分支和右分支究竟是表示 0 还是表示 1 没有明确规定)。
利用哈夫曼二叉树可以设计出总长度最短的二进制前缀编码。WPL 可视为最终编码得到的二进制编码长度。哈夫曼编码的加权平均长度为 $\frac{WPL}{所有叶结点权值之和}$。
判定某字符集的不等长编码是否具有前缀特性的过程
二叉树既可用于保存各字符的编码(二进制),又可用于检测编码是否具有前缀特性。判定编码是否具有前缀特性的过程,也是构建二叉树的过程。初始时,二叉树中仅含有根结点,其左子指针和右子指针均为空。依次读入每个编码 C,建立/寻找从根开始对应于该编码的一条路径,过程如下:
对每个编码,从左至右扫描 C 的各位,根据 C 的当前位(0 或 1)沿结点的指针(左子指针或右子指针)向下移动。当遇到空指针时,创建新结点,让空指针指向该新结点并继续移动。沿指针移动的过程中,可能遇到三种情况:
① 若遇到了叶结点(非根),则表明不具有前缀特性,返回。
② 若在处理 C 的所有位的过程中,均没有创建新结点,则表明不具有前缀特性,返回。
③ 若在处理 C 的最后一个编码位时创建了新结点,则继续验证下一个编码。
若所有编码均通过验证,则编码具有前缀特性。
并查集
一种简单的集合表示。是一种用于管理元素分组的数据结构,主要用于处理不相交集合的合并与查询等问题。
基本操作
initial(S):将集合 S 中的每个元素都初始化为只有一个单元素的子集合。
union(S, Root1, Root2):把集合 S 中的子集合 Root2 并入子集合 Root1。
要求 Root1 和 Root2 互不相交,否则不执行合并。
find(S, x):查找集合 S 中单元素 x 所在的子集合,并返回该子集合的根结点。
存储结构
通常使用树(森林)的双亲表示作为并查集的存储结构。
通常用数组元素的下标代表元素名,用根结点的下标代表子集合名,根结点的双亲域为负数(可设置为该子集合元素数量的相反数)。
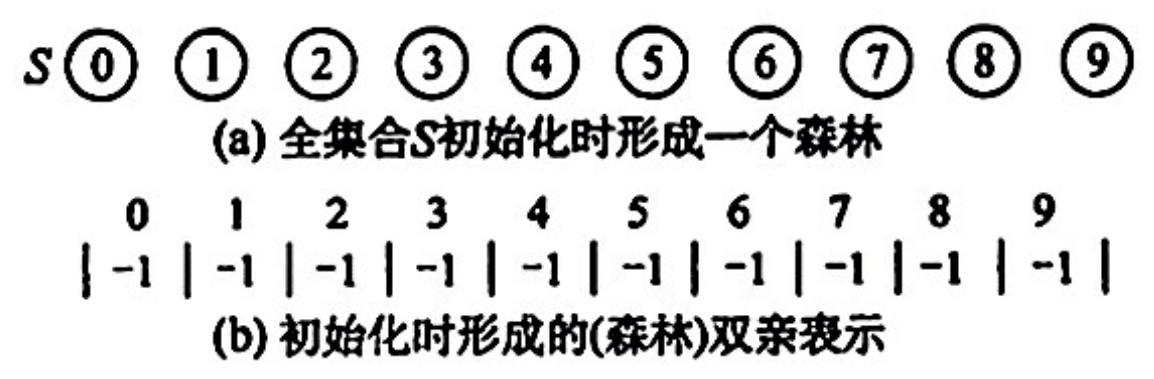
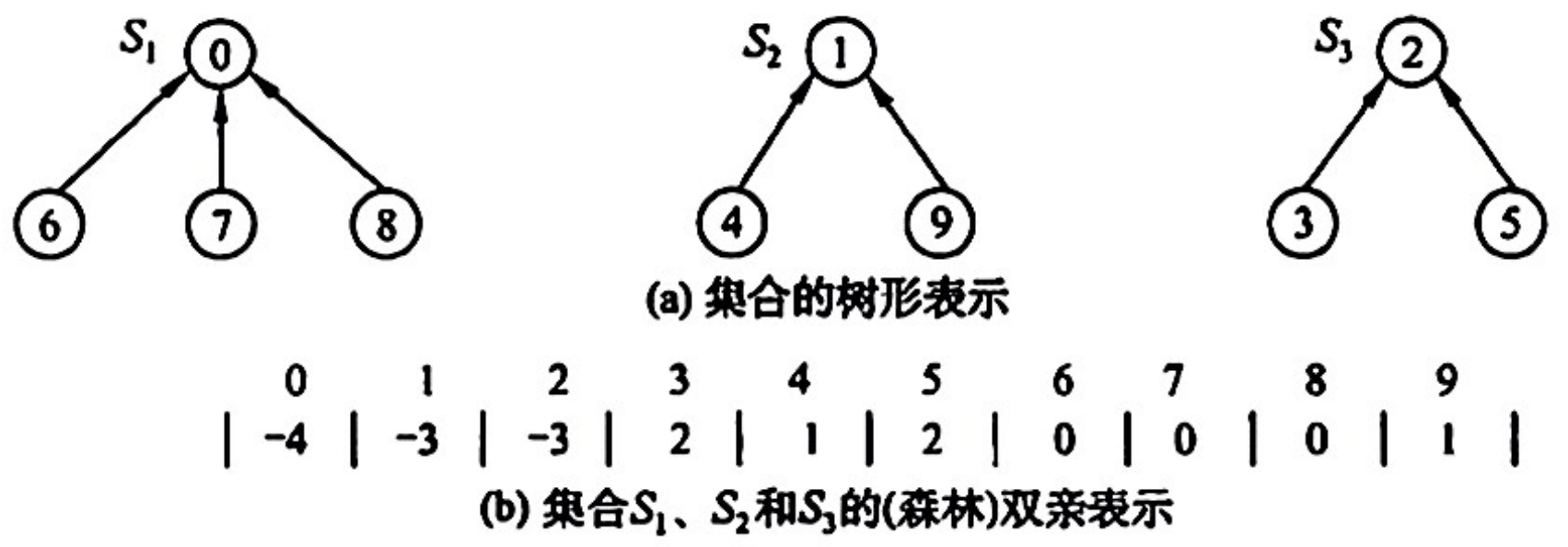
为了得到两个子集合的并,只需将其中一个子集合根结点的双亲指针指向另一个集合的根结点。
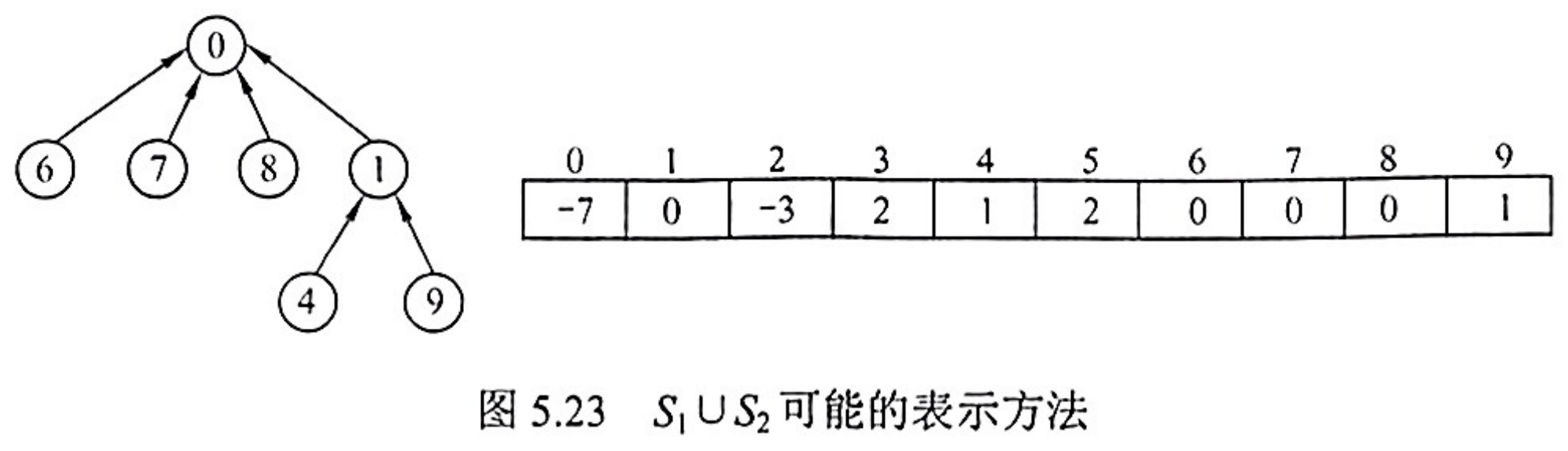
改进的 union 操作
极端情况下,$n$ 个元素构成的集合树的深度为 $n$,则 find 操作的最坏时间复杂度为 O(n)。改进的办法是,在做 union 操作之前,首先判别子集中的成员数量,然后令成员少的根指向成员多的根,即把小树合并到大树。为此需要令根结点的绝对值保存集合树中的成员数量。采用这种方法构造得到的集合树,其深度不超过 $\left\lfloor\log _2 n\right\rfloor+1$。
改进的 find 操作
当所查元素 x 不在树的第二层时,在算法中增加一个 “压缩路径” 的功能,将从根到元素 x 路径上的所有元素都变成根的孩子。
通过 find 操作的 “压缩路径” 优化后,可使集合树的深度不超过 O(α(n)),其中 α(n) 是一个增长极其缓慢的函数,对于常见的正整数 n,通常 α(n) ≤ 4。
并查集与图
并查集可以检测图中是否存在环路的问题
依次探测图的各条边,用并查集检查该边依附的两个顶点是否已属于同一集合(两个顶点的根结点是否相同)。若是,则说明图中存在环路。
并查集可用于实现 Kruskal 算法
在用并查集实现 Kruskal 算法求图的最小生成树时:哦按段是否加入一条边之前,先查找这条边关联的两个顶点是否属于同一个集合(即判断加入这条边之后是否形成回路),若形成回路,则继续判断下一条边;若不形成回路,则将该边和边对应的顶点加入最小生成树 T,并继续判断下一条边,直到所有顶点都已加入最小生成树 T。
并查集可用于判断无向图的连通性
用并查集判断无向图连通性的方法:遍历无向图的边,每遍历到一条边,就把这条边连接的两个顶点合并到同一个集合中,处理完所有边后,只要相互连通的顶点就会被合并到同一个子集合中,相互不连通的顶点一定在不同的子集合中。
刷题总结
完全二叉树只要知道总结点个数就能知道 $n_0$、$n_1$、$n_2$ 各为多少
完全二叉树中 $n_1$ 只可能是 0 或 1,而二叉树 $n_0+n_2$ 必为奇数($n_0=1+n_2$),因此可以根据总结点数的奇偶性来确定 $n_1$,进而确定 $n_0$ 和 $n_2$
也就是说,当完全二叉树总结点数为 $2n$ 时,$n_0=n$, $n_1=1$,$n_2=n-1$;总结点数为 $2n-1$ 时,$n_0=n$, $n_1=0$,$n_2=n-1$
高度为 $h$ 的完全二叉树最少有 $2^{h-1}$ 个结点,最多有 $2^h-1$ 个结点
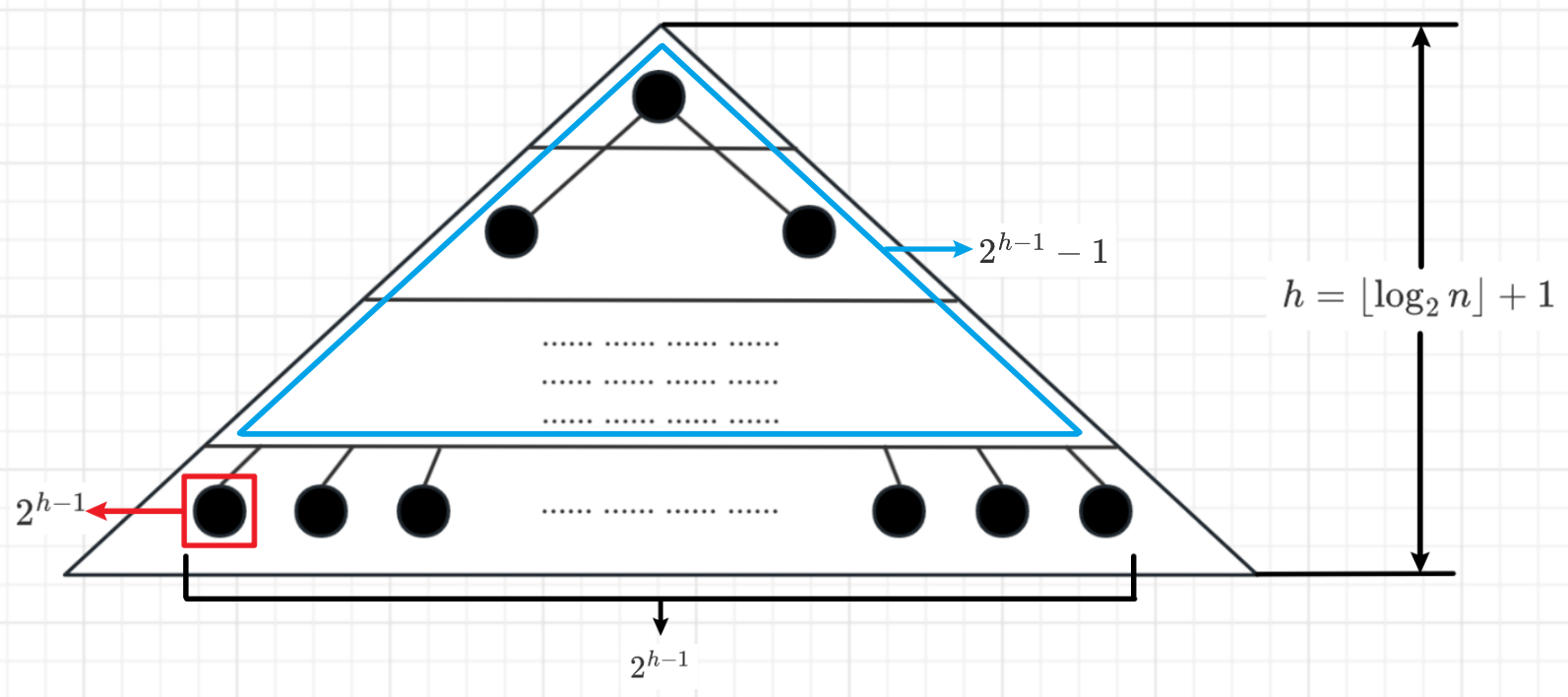
高度为 $h$ 的 $m$ 叉树至多有 $\frac{m^h-1}{m-1}$ 个结点
具有 $n$ 个结点的 $m$ 叉树的最小高度为 $\lceil\log_m(n(m-1)+1)\rceil$(二叉树为 $\lceil\log_2(n+1)\rceil$ 或 $\lfloor\log_2n\rfloor+1$)
满 $m$ 叉树
编号为 $i$ 的结点的双亲结点(若存在)的编号是 $\lfloor\frac{i-1}{m}\rfloor+1$
编号为 $i$ 的结点的第 $k$ 个孩子结点(若存在)的编号是 $(i-1)m+k+1$
编号为 $i$ 的结点有右兄弟的条件是 $(i-1)\% m \neq 0$
Catalan 数(卡特兰数)应用
$f(n)=\frac{C^n_{2n}}{n+1}=\frac{(2 n) !}{n !(n+1) !}$
1)$n$ 个不同元素入栈序列确定,并可在任意时刻出栈,可能的不同出栈序列数目(出入栈反过来也一样)。
2)给定 $n$ 个结点,可能构成的不同形态的二叉树数目。
3)先序序列给定,可能的不同中序序列/二叉树数目。
4)中序序列给定,可能的不同先序序列/二叉树数目;$n$ 个不同结点构造的二叉排序树形态数目。
5)$n$ 对括号,可能的括号匹配序列数目。
线索二叉树是物理结构。
线索二叉树至多两个空链域,至少一个空链域。
先序线索化后至少 1 个空链域(最右叶结点右链域),若根结点无左子树,则是 2 个空链域。
中序线索化后有 2 个空链域(最左结点左链域、最右结点右链域)。
后序线索化后至少 1 个空链域(最左叶结点左链域),若根结点无右子树,则是 2 个空链域。
存在单树森林
🔥对于一棵树:
“分支” 数 = 叶结点数 = 无孩子 = 有右兄弟结点数 + 1
非叶结点数 = 有孩子 = 无右兄弟结点数 - 1(每个非叶结点的最右孩子以及根结点没有右兄弟)
对于森林,如果将所有树的根结点视为兄弟,则上述规律依然适用。
树和森林只有两种遍历:先根、后根,对应二叉树遍历为:先序、中序
森林的后根遍历有时也叫后序遍历、中序遍历、中根遍历。
考题默认哈夫曼树是二叉。
不可能的哈夫曼编码:非前缀编码、频率和长度不匹配(实在不行就画)。
最多编码:尽可能使叶结点都处于最底层。
合并两个长度分别为 $m$ 和 $n$ 的有序表,最坏情况下需要比较 $m+n-1$ 次。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZERO!
